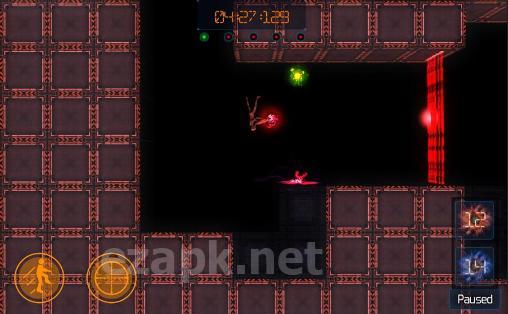
Kyport: Portals. Dimensions

Willkommen in Kyport, wo Sie verschiedene Portale und Dimensionen erkunden, um die lebenswichtige grüne Substanz zu sammeln, die zur Wiederherstellung des Gleichgewichts im Universum erforderlich ist. Ihr Ziel ist es, so schnell wie möglich die gesamte grüne Substanz in jeder Dimension zu sammeln. Um Ihre Reise zu erleichtern, können Sie Portale auf ebenen Flächen erstellen, um schnell zwischen zwei Punkten zu reisen. Sie haben auch die Möglichkeit, Portale zu parallelen Dimensionen zu öffnen. Seien Sie jedoch darauf vorbereitet, in diesem Android-Spiel auf zahlreiche Hindernisse und Fallen zu stoßen. Nutzen Sie Ihre Fähigkeiten, um Objekte zu bewegen und tödlichen Laserstrahlen auszuweichen, um durch die 20 herausfordernden Level zu kommen. Mit seiner lebendigen Grafik, den vielfältigen Rätseln und dem fesselnden Gameplay wird Kyport Sie mit Sicherheit unterhalten.<|endoftext|><|endoftext|> # 2015 AMC 10A Probleme/Problem 1. ## Inhalt. 1 Problem 2 Lösung 3 Videolösung 4 Siehe auch ## Problem Welchen Wert hat \[2-4+6-8+10-12+14-16+18-20?\] $\textbf{(A)}\ -10\qquad\textbf{(B)}\ -2\qquad\textbf{(C)}\ 0\qquad\textbf{(D)}\ 2\qquad\textbf{ (E)}\ 10$ ## Lösung. Wir können die Terme neu anordnen, um \[2+6+10+14+18-4-8-12-16-20.\] zu erhalten. Jetzt können wir die Terme paaren, um \[(2-2)+( 6-4)+(10-8)+(14-12)+(18-16)-20.\] Vereinfacht erhalten wir \[0+2+2+2+2-20=10-20=\boxed{\textbf{(A)}\ -10}.\] ## Videolösung. https://youtu.be/8-3XeJXm-q0 ~ Savannahsolver <|endoftext|>## Mathematische Foren ## Kategorie: Oberstufenolympiaden ## Thema: Ungleichheit ## Aufrufe: 338 ## [Eingabe: math-user1, num_posts=697, num_likes_received=372] ## [math-user1, num_likes=1] Sei $a,b,c>0$. Beweisen Sie das $\frac{a^2}{b}+\frac{b^2}{c}+\frac{c^2}{a}+3\sqrt[3]{abc}\geq 2(a+b +c)$ ## [Eingabe: math-user2, num_posts=545, num_likes_received=72] ## [math-user2, num_likes=0] Nach AM-GM gilt $\frac{a^2}{b}+\frac{a^2}{b}+b\ge3a$ und ähnliches für andere, also haben wir $\sum_{cyc}\frac{ a^2}{b}+a+b+c\ge3(a+b+c)$ $\impliziert