Pixelo

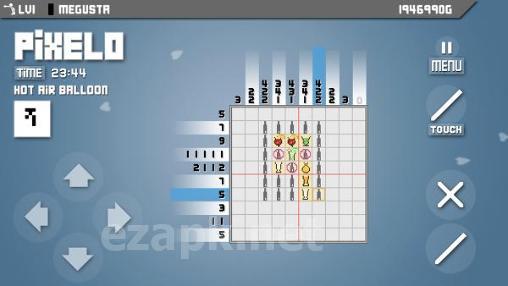
Pixelo ist ein Android-Spiel, bei dem Sie Ihre Logik und Fantasie einsetzen, um Rätsel zu lösen, indem Sie Kacheln auf dem Bildschirm ausmalen, um ein Bild zu erstellen. Das Raster kann zwischen 5 x 5 und 20 x 20 Kacheln umfassen und jede Spalte und Zeile enthält Zahlen, die angeben, wie viele Kacheln ausgefüllt werden müssen. Die farbigen Kachelgruppen müssen durch mindestens eine leere Kachel getrennt sein. Mit über 500 Rätseln, toller Grafik, einfacher Steuerung, hohen Punktzahlen und fesselndem Gameplay ist Pixelo ein Spiel, das man unbedingt ausprobieren muss.<|endoftext|><|endoftext|> # 2015 AMC 10A Probleme/Problem 1. ## Inhalt. 1 Problem 2 Lösung 3 Videolösung 4 Siehe auch ## Problem Welchen Wert hat \[2-4+6-8+10-12+14-16+18-20+22?\] $\textbf{(A)}\ -110\qquad\textbf{(B)}\ -44\qquad\textbf{(C)}\ 0\qquad\textbf{(D)}\ 22\qquad\textbf{ (E)}\ 110$ ## Lösung. Wir können die Terme neu anordnen, um \[2+6+10+14+18+22-4-8-12-16-20.\] zu erhalten. Jetzt können wir die Terme paaren, um \[(2+22) zu erhalten. +(6+18)+(10+14)-4-8-12-16-20.\] Vereinfacht erhalten wir \[24+24+24-60=\boxed{\textbf{(C)}\ 0}.\] ## Videolösung. https://youtu.be/8zQNG5RZuJw ~ Savannahsolver <|endoftext|>## Mathematische Foren ## Kategorie: Oberstufenolympiaden ## Thema: Ungleichheit ## Aufrufe: 338 ## [Eingabe: math-user1, num_posts=697, num_likes_received=372] ## [math-user1, num_likes=1] Sei $a,b,c>0$. Beweisen Sie das $\frac{a^2}{b}+\frac{b^2}{c}+\frac{c^2}{a}+3\sqrt[3]{abc}\geq 2(a+b +c)$ ## [Eingabe: math-user2, num_posts=545, num_likes_received=72] ## [math-user2, num_likes=0] Nach AM-GM gilt $3\sqrt[3]{abc}\ge a+b+c$ und nach Cauchy-Schwarz gilt $\frac{a^2}{b}+\frac{b^2}{c} +\frac{c^2}{a}\ge\frac{(a+b+c)^2}{a+b+c}=a+b+c$ also $LHS\ge2(a+b+ c)$ ## [math-user1, num_likes=1] [quote=math-user2]Von