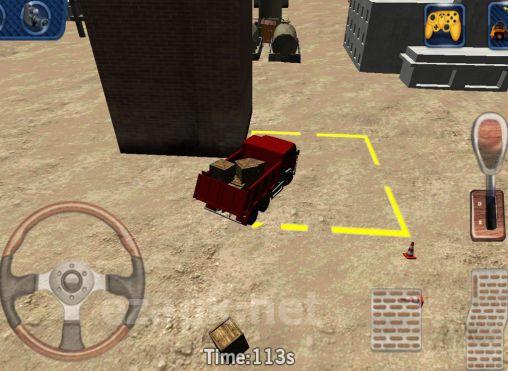
Heavy truck 3D: Cargo delivery

Erleben Sie den Nervenkitzel eines LKW -Fahrers auf einer Baustelle mit dem Game Heavy Truck 3D: Frachtlieferung. Dieses Spiel bietet 20 aufregende Levels und ein realistisches Steuerungssystem, mit dem Sie sich wie hinter dem Lenkrad fühlen. Meister Sie die präzissten Park- und Entladetechniken und fordern Sie sich mit dem Zeitspielmodus heraus. Der Begriff "Seelenverwandter" wird oft verwendet, um eine Person zu beschreiben, die idealerweise als engen Freund oder romantischer Partner geeignet ist. Es wird angenommen, dass ein Seelenverwandter jemand eine tiefe Verbindung mit einer anderen Person hat, die oft als spirituelle oder emotionale Bindung beschrieben wird. Diese Verbindung soll die physische Anziehungskraft überwinden und basiert auf einem starken Gefühl der Kompatibilität, des Verständnisses und des gegenseitigen Respekts. Einige Menschen glauben, dass Seelenverwandte dazu bestimmt sind, sich zu treffen und dass ihre Beziehung sein soll. Andere sehen Seelenverwandte als Individuen, die einen tiefgreifenden Einfluss auf das Leben des anderen haben und ihnen helfen, sich als Individuen zu entwickeln. Letztendlich ist das Konzept eines Seelenverwandten subjektiv und kann für verschiedene Menschen unterschiedliche Dinge bedeuten. <| Endoftext |> ## Mathematische Foren ## Kategorie: High School Olympiaden ## Thema: Ungleichheit ## Ansichten: 338 ## [ENTER: Math-User1, num_posts = 697, num_likes_received = 372] ## [Math-User1, num_likes = 1] Sei $ a, b, c> 0 $. Beweisen Sie das $ \ frac {a^2} {b}+\ frac {b^2} {c}+\ frac {c^2} {a} +3 \ sqrt [3] {abc} \ Geq 2 (a+b +c) $ ## [ENTER: Math-User2, num_posts = 545, num_likes_received = 72] ## [Math-User2, num_likes = 0] Von am-gm haben: $ \ frac {a^2} {b}+\ frac {a^2} {b}+b \ ge3a $ und ähnlich sind wir: $ \ sum_ {cyc} \ frac {a^2 } oder c) $ $ \ impliziert $ 3 \ sqrt [3] {abc} \ Ge A+B+C $, was durch AM-GM offensichtlich ist ## [Math-User1, num_likes = 1] [quote = math-user2] von am-gm haben: $ \ frac {a^2} {b}+\ frac {a^2} {b}+b \ ge3a $ und ähnlich wir bekommen: $ \ sum_ {cyc } \ frac {a^2} {b}+a+b \ ge3 (a+b+c) $ und wir müssen beweisen, dass: $ 3 (a+b+c) +3 \ sqrt [3] {abc} \ Ge2 (A+B+C) $ $ \ impliziert $ 3 \ sqrt [3] {abc} \ Ge A+B+C $, was durch AM-GM [/QUOTE "offensichtlich ist