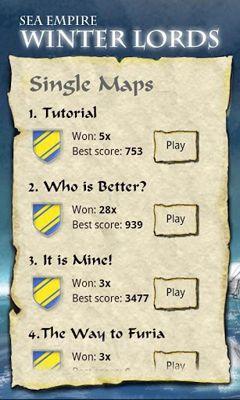
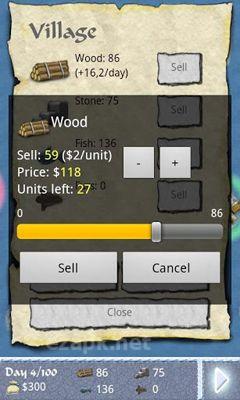
Sea Empire: Winter lords

„Begeben Sie sich in Sea Empire: Winter Lords auf die Eroberung nahegelegener Inseln, indem Sie eine beeindruckende Flotte aufbauen. Dieses Spiel besticht durch einfache Grafiken und bietet verschiedene Schiffsoptionen.“<|endoftext|><|endoftext|> # 2006 AMC 12B Probleme/Problem 1. (Weitergeleitet von 2006 AMC 12B Probleme / Problem 1) ## Problem. Was ist der Wert von $2^{-3}+3^{-3}+4^{-3}+...+2006^{-3}+2007^{-3}$? $\text {(A) } \frac{2007}{2^3} \qquad \text {(B) } \frac{2007^2}{2^3} \qquad \text {(C) } \frac {2007^2+2007}{2^3} \qquad \text {(D) } \frac{2007^2+2007}{2^6} \qquad \text {(E) } \frac{2007^2+2007}{2^7}$ ## Lösung. Wir können den Ausdruck umschreiben als \begin{align*} 2^{-3}+3^{-3}+4^{-3}+...+2006^{-3}+2007^{-3} &= \left(2 ^{-3}+3^{-3}+4^{-3}+...+2006^{-3}\right) + 2007^{-3} \\ &= \left(\frac{1}{2^3}+\frac{1}{3^3}+\frac{1}{4^3}+...+\frac{1}{2006^3} \right) + \frac{1}{2007^3} \\ &= \frac{1}{8}+\frac{1}{27}+\frac{1}{64}+...+\ frac{1}{2006^3} + \frac{1}{2007^3} \\ &= \left(\frac{1}{2^3}\right)^3+\left(\frac{1}{3^3}\right)^ 3+\left(\frac{1}{4^3}\right)^3+...+\left(\frac{1}{2006^3}\right)^3 + \left(\frac{1}{2007^3}\right)^3 \\ &= \left(\frac{1}{2^3}+\frac{1}{3^3}+\frac{ 1}{4^3}+...+\frac{1}{2006^3}+\frac{1}{2007^3}\right)^3 \\ &= \left(\frac{1}{8}+\frac{1}{27}+\frac{1}{64}+...+\frac{1}{2006^3}+\frac{1} {2007^3}\right)^3 \\ &= \left(\frac{1}{8}+\frac{1}{27}+\frac