Plush Wars

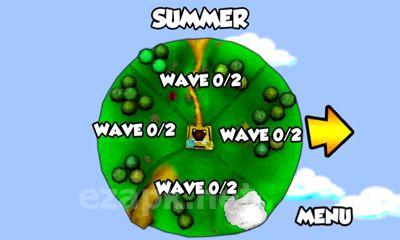
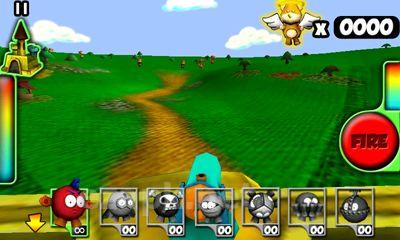
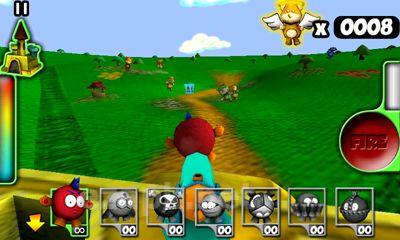
Bienvenido a Plush Wars, donde tu misión es proteger el castillo de la Princesa Plushlandia y a la propia princesa de una invasión de zombis de peluche. En este lujoso país, la única arma real es una pistola, mientras que todo lo demás, incluidas las municiones, está hecho de material lujoso. Desde todas las direcciones, te enfrentarás a osos de peluche y perritos que se han convertido en zombis, muy probablemente debido a que niños traviesos les arrancaron los ojos, las patas y la cabeza. Tu arma preferida es una pistola cargada con balas de peluche. Su primer paso es seleccionar su objetivo y luego presionar el botón para disparar.<|endoftext|><|endoftext|> # 2015 AMC 10A Problemas/Problema 1. ## Contenidos. 1 problema 2 solución 3 Solución de vídeo 4 Ver también ## Problema ¿Cuál es el valor de \[2-4+6-8+10-12+14-16+18-20?\] $\textbf{(A)}\ -10\qquad\textbf{(B)}\ -2\qquad\textbf{(C)}\ 0\qquad\textbf{(D)}\ 2\qquad\textbf{ (E)}\ 10$ ## Solución. Podemos reordenar los términos para obtener \[2+6+10+14+18-4-8-12-16-20.\] Ahora, podemos emparejar los términos para obtener \[(2-2)+( 6-4)+(10-8)+(14-12)+(18-16)-20.\] Simplificando, obtenemos \[0+2+2+2+2-20=10-20=\boxed{\textbf{(A)}\ -10}.\] ## Solución de vídeo. https://youtu.be/8-3XeJXm-qE ~ solucionador de sabana <|endoftext|>## Foros de Matemáticas ## Categoría: Olimpíadas de secundaria ## Tema: Desigualdad ## Vistas: 338 ## [ingrese: math-user1, num_posts=697, num_likes_received=372] ## [usuario-matemático1, num_likes=1] Deje $a,b,c>0$. demostrar que $\frac{a^2}{b}+\frac{b^2}{c}+\frac{c^2}{a}+3\sqrt[3]{abc}\geq 2(a+b) +c)$ ## [ingrese: math-user2, num_posts=545, num_likes_received=72] ## [usuario-matemático2, num_likes=0] Por AM-GM tenemos:$\frac{a^2}{b}+\frac{a^2}{b}+b\ge3a$ y similar obtenemos:$\sum_{cyc}\frac{a^2 }{b}+a+b\ge3(a+b+c)$ $\implica$ $\sum_{cyc}\frac{a^2