Putter King Adventure Golf

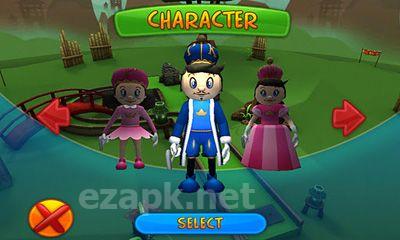
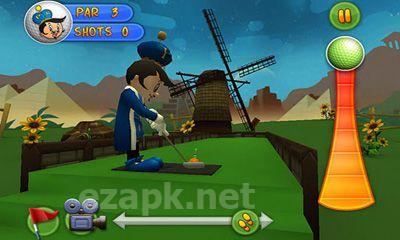
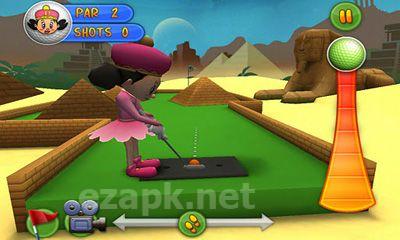
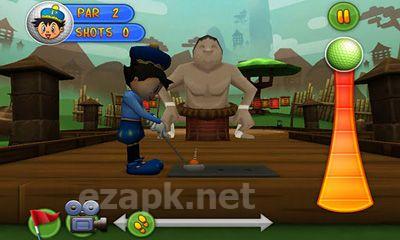
Putter King Adventure Golf es un juego de golf en 3D de primer nivel. Cuenta con gráficos de alta calidad y un sonido impresionante. Los cursos están ubicados en todo el mundo. También puedes compartir tus resultados con amigos en Facebook y Twitter. Elige entre una variedad de entretenidos personajes animados, cada uno con sus propias habilidades únicas. Tu objetivo es hacer avanzar la pelota a través de varios obstáculos hasta llegar al hoyo. El juego ofrece 24 hoyos temáticos distintos, así como 3 hoyos creados por el usuario y 4 modos de juego (campeonato, cronometrado, multijugador y entrenamiento).<|endoftext|><|endoftext|> # 2015 AMC 10B Problemas/Problema 1. ## Contenidos. 1 problema 2 solución 3 Solución de vídeo 4 Ver también ## Problema. ¿Cuál es el valor de $2+4+6+8+10+12+14+16+18+20$? $\textbf{(A)}\ 90\qquad\textbf{(B)}\ 100\qquad\textbf{(C)}\ 110\qquad\textbf{(D)}\ 120\qquad\textbf{(E )}\ 130$ ## Solución. Podemos emparejar los números de la siguiente manera: $(2+20)+(4+18)+(6+16)+(8+14)+(10+12)$. Cada par suma $22$, y hay $5$ pares, por lo que la suma es $22 \cdot 5 = \boxed{\textbf{(B)}\ 100}$. ## Solución de vídeo. https://youtu.be/8WrdYLw9_ns ~ solucionador de sabana <|endoftext|>## Foros de Matemáticas ## Categoría: Olimpíadas de secundaria ## Tema: Desigualdad ## Vistas: 338 ## [ingrese: math-user1, num_posts=697, num_likes_received=372] ## [usuario-matemático1, num_likes=1] Deje $a,b,c>0$. demostrar que $\frac{a^2}{b}+\frac{b^2}{c}+\frac{c^2}{a}+3\sqrt[3]{abc}\geq 2(a+b) +c)$ ## [ingrese: math-user2, num_posts=545, num_likes_received=72] ## [usuario-matemático2, num_likes=0] Por AM-GM tenemos:$\frac{a^2}{b}+\frac{a^2}{b}+b\ge3a$ y similar obtenemos:$\frac{a^2}{b}+ \frac{b^2}{c}+\frac{c^2}{a}\ge a+b+c$ y por AM-GM nuevamente:$3\sqrt[3]{abc}\ge3\frac{ 3abc}{a+b+c}$ entonces deberíamos demostrar que:$\frac{a^2}{b}+\frac{b^2}{c}+\frac{c^2}{a}