Block puzzle pop

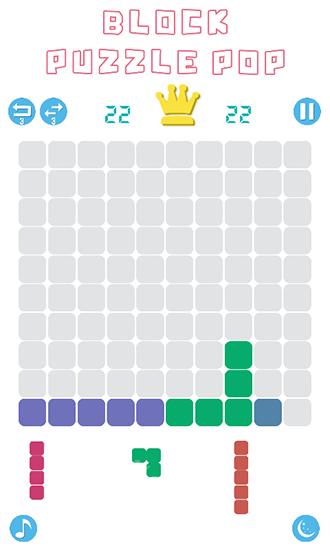
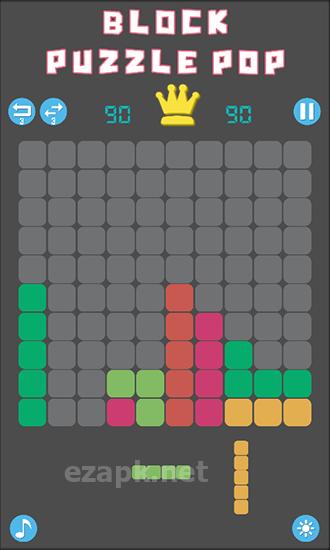
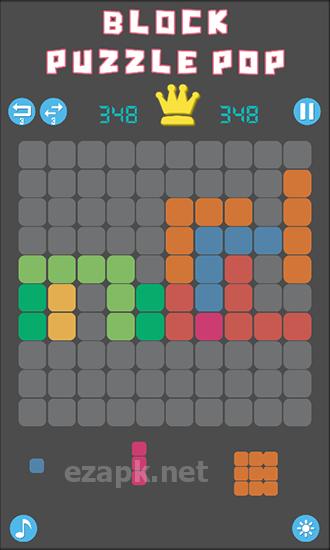
En el juego "Bloque Puzzle Pop", debes colocar estratégicamente bloques de varias formas, todas compuestas de cuadrados. Su objetivo es crear filas completas de bloques para eliminarlos. Use su pensamiento lógico e imaginación espacial para conquistar niveles desafiantes en este juego de Android. En la parte inferior de la pantalla, verá tres bloques que aparecerán a continuación. Simplemente arrastre estos bloques a la pantalla y colóquelos en cualquier espacio disponible. Tómese su tiempo y planifique cuidadosamente sus movimientos, ya que no hay límite de tiempo en este juego. Las características del juego incluyen gráficos minimalistas, un modo de día y noche, tablas de clasificación y 15 logros para desbloquear. <| Endoftext |> <| endoftext |> <| endoftoxt |> # 2006 AMC 12B Problemas/Problema 1. (Redirigido de los problemas de 2006 AMC 12B / Problema 1) ## Problema. ¿Cuál es el valor de $ 2^{-3} +3^{-3} $? $ \ text {(a)} \ frac {5} {9} \ qquad \ text {(b)} \ frac {17} {24} \ qquad \ text {(c)} \ frac {19} {24} \ Qquad \ text {(d)} \ frac {7} {8} \ qquad \ text {(e)} \ frac {11} {12} $ ## Solución. Podemos reescribir $ 2^{-3} $ y $ 3^{-3} $ como $ \ frac {1} {2^3} $ y $ \ frac {1} {3^3} $, respectivamente. Luego, podemos combinar las fracciones para obtener $ \ frac {1} {8}+\ frac {1} {27} $. Podemos encontrar un denominador común de $ 216 $ para obtener $ \ frac {27} {216}+\ frac {8} {216} = \ frac {35} {216} $. Podemos simplificar esta fracción para obtener $ \ boxed {\ textbf {(b)} \ frac {17} {24}} $. <| endoftext |> ## Foros matemáticos ## Categoría: Olimpiadas de secundaria ## Tema: Desigualdad ## Vistas: 351 ## [Enter: Math-User1, num_posts = 697, num_likes_RECeive = 372] ## [Math-user1, num_likes = 1] Deje que $ A, B, C $ sea números reales positivos de tal manera que $ A+B+C = 3 $. Demostrar que $ \ frac {a} {b}+\ frac {b} {c}+\ frac {c} {a} +3 \ geq 2 (a^2+b^2+c^2) $ ## [Enter: Math-user2, num_posts = 467, num_likes_RECeive = 180] ## [Math-user2, num_likes = 0] Por am-gm, $ \ frac {a} {b}+\ frac {a} {b}+\ frac {b} {c} \ ge3 \ sqrt [3] {\ frac {a^2} {bc} } = \ frac {3a} {\ sqrt [3] {ABC}} $. Summar cíclicamente da $ \ frac {a} {b}+\ frac {b} {c