Plush Wars

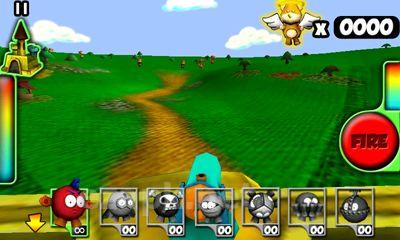
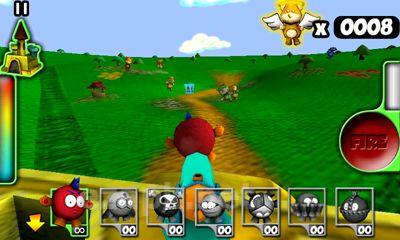
Bienvenue dans Plush Wars, où votre mission est de protéger le château de la princesse Plushlandia et la princesse elle-même d'une invasion de zombies en peluche. Dans ce pays luxueux, la seule véritable arme est une arme à feu, tandis que tout le reste, y compris les munitions, est fabriqué à partir de matériaux pelucheux. De toutes les directions, vous serez confronté à des ours en peluche et à des toutous transformés en zombies, probablement à cause d'enfants espiègles qui leur ont arraché les yeux, les pattes et la tête. Votre arme de choix est une arme chargée de balles en peluche. Votre première étape consiste à sélectionner votre cible, puis à appuyer sur le bouton pour tirer.<|endoftext|><|endoftext|> # 2015 AMC 10A Problèmes/Problème 1. ## Contenu. 1 Problème 2 solutions 3 Solutions vidéo 4 Voir aussi ## Problème Quelle est la valeur de \[2-4+6-8+10-12+14-16+18-20 ?\] $\textbf{(A)}\ -10\qquad\textbf{(B)}\ -2\qquad\textbf{(C)}\ 0\qquad\textbf{(D)}\ 2\qquad\textbf{ (E)}\ 10$ ## Solution. Nous pouvons réorganiser les termes pour obtenir \[2+6+10+14+18-4-8-12-16-20.\] Maintenant, nous pouvons associer les termes pour obtenir \[(2-2)+( 6-4)+(10-8)+(14-12)+(18-16)-20.\] En simplifiant, on obtient \[0+2+2+2+2-20=10-20=\boxed{\textbf{(A)}\ -10}.\] ## Solution vidéo. https://youtu.be/8-3XeJXm-qE ~ résolveur de savane <|endoftext|>## Forums mathématiques ## Catégorie: Olympiades des lycées ## Sujet : Inégalités ## Vues: 338 ## [entrez: math-user1, num_posts=697, num_likes_received=372] ## [math-user1, num_likes=1] Soit $a,b,c>0$. Prouvez que $\frac{a^2}{b}+\frac{b^2}{c}+\frac{c^2}{a}+3\sqrt[3]{abc}\geq 2(a+b +c)$ ## [entrez: math-user2, num_posts=545, num_likes_received=72] ## [math-user2, num_likes=0] Par AM-GM ont:$\frac{a^2}{b}+\frac{a^2}{b}+b\ge3a$ et similaire nous obtenons:$\sum_{cyc}\frac{a^2 }{b}+a+b\ge3(a+b+c)$ $\implies$ $\sum_{cyc}\frac{a^2