Block puzzle pop

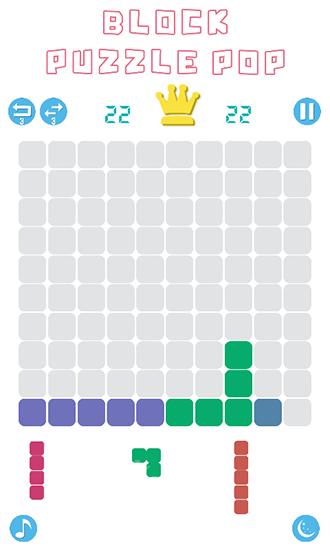
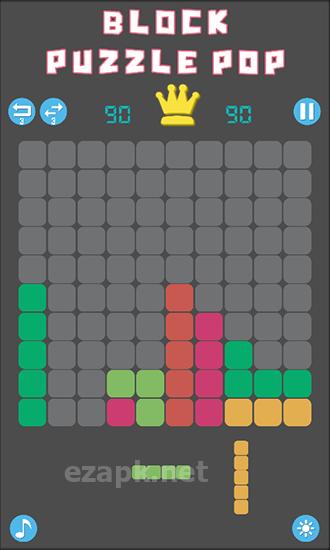
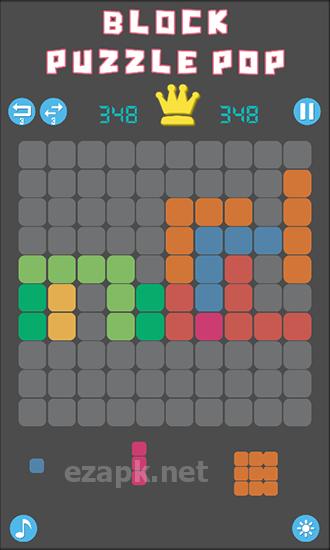
Dans le jeu "Block Puzzle Pop", vous devez placer stratégiquement des blocs de différentes formes, tous composés de carrés. Votre objectif est de créer des rangées complètes de blocs afin de les éliminer. Utilisez votre pensée logique et votre imagination spatiale pour conquérir des niveaux difficiles dans ce jeu Android. En bas de l'écran, vous verrez trois blocs qui apparaîtront ensuite. Faites simplement glisser ces blocs sur l'écran et positionnez-les dans n'importe quel espace disponible. Prenez votre temps et planifiez soigneusement vos mouvements, car il n'y a pas de limite de temps dans ce jeu. Les fonctionnalités du jeu incluent des graphiques minimalistes, un mode de jour et de nuit, des classements et 15 réalisations à déverrouiller. <| Endoftext |> <| endoftext |> <| endoftext |> # 2006 Problèmes AMC 12B / Problème 1. (Redirigé à partir des problèmes AMC 12B 2006 / Problème 1) ## Problème. Quelle est la valeur de 2 $ ^ {- 3} +3 ^ {- 3} $? $ \ text {(a)} \ frac {5} {9} \ qquad \ text {(b)} \ frac {17} {24} \ qquad \ text {(c)} \ frac {19} {24} \ qquad \ text {(d)} \ frac {7} {8} \ qquad \ text {(e)} \ frac {11} {12} $ ## Solution. Nous pouvons réécrire $ 2 ^ {- 3} $ et $ 3 ^ {- 3} $ as $ \ frac {1} {2 ^ 3} $ et $ \ frac {1} {3 ^ 3} $, respectivement. Ensuite, nous pouvons combiner les fractions pour obtenir $ \ frac {1} {8} + \ frac {1} {27} $. Nous pouvons trouver un dénominateur commun de 216 $ $ pour obtenir $ \ frac {27} {216} + \ frac {8} {216} = \ frac {35} {216} $. Nous pouvons simplifier cette fraction pour obtenir $ \ boxed {\ textBf {(b)} \ frac {17} {24}} $. <| endoftext |> ## Forums mathématiques ## Catégorie: Olympiades du secondaire ## Sujet: inégalité ## Vues: 351 ## [Entrée: math-user1, num_posts = 697, num_likes_received = 372] ## [math-user1, num_likes = 1] Soit $ a, b, c $ nombres réels positifs tels que $ a + b + c = 3 $. Prouver que $ \ frac {a} {b} + \ frac {b} {c} + \ frac {c} {a} +3 \ geq 2 (a ^ 2 + b ^ 2 + c ^ 2) $ ## [Entrée: math-user2, num_posts = 467, num_likes_received = 180] ## [math-user2, num_likes = 0] Par am-gm, $ \ frac {a} {b} + \ frac {a} {b} + \ frac {b} {c} \ ge3 \ sqrt [3] {\ frac {a ^ 2} {bc} } = \ frac {3a} {\ sqrt [3] {ABC}} $. Summing Cycliquement donne $ \ frac {a} {b} + \ frac {b} {c