Pixelo

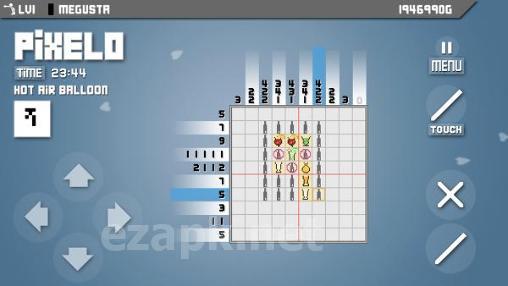
Pixelo est un jeu Android dans lequel vous utilisez votre logique et votre imagination pour résoudre des énigmes en coloriant des tuiles sur l'écran pour créer une image. La grille peut aller de 5x5 à 20x20 tuiles et chaque colonne et ligne comporte des chiffres indiquant le nombre de tuiles à remplir. Les groupes de tuiles colorées doivent être séparés par au moins une tuile vierge. Avec plus de 500énigmes, de superbes graphismes, des commandes simples, des scores élevés et un gameplay captivant, Pixelo est un jeu incontournable.<|endoftext|><|endoftext|> # 2015 AMC 10A Problèmes/Problème 1. ## Contenu. 1 Problème 2 solutions 3 Solutions vidéo 4 Voir aussi ## Problème Quelle est la valeur de \[2-4+6-8+10-12+14-16+18-20+22 ?\] $\textbf{(A)}\ -110\qquad\textbf{(B)}\ -44\qquad\textbf{(C)}\ 0\qquad\textbf{(D)}\ 22\qquad\textbf{ (E)}\ 110$ ## Solution. Nous pouvons réorganiser les termes pour obtenir \[2+6+10+14+18+22-4-8-12-16-20.\] Maintenant, nous pouvons associer les termes pour obtenir \[(2+22) +(6+18)+(10+14)-4-8-12-16-20.\] En simplifiant, on obtient \[24+24+24-60=\boxed{\textbf{(C)}\ 0}.\] ## Solution vidéo. https://youtu.be/8zQNG5RZuJw ~ résolveur de savane <|endoftext|>## Forums mathématiques ## Catégorie: Olympiades des lycées ## Sujet : Inégalités ## Vues: 338 ## [entrez: math-user1, num_posts=697, num_likes_received=372] ## [math-user1, num_likes=1] Soit $a,b,c>0$. Prouvez que $\frac{a^2}{b}+\frac{b^2}{c}+\frac{c^2}{a}+3\sqrt[3]{abc}\geq 2(a+b +c)$ ## [entrez: math-user2, num_posts=545, num_likes_received=72] ## [math-user2, num_likes=0] Par AM-GM ayez $3\sqrt[3]{abc}\ge a+b+c$ et par Cauchy-Schwarz ayez $\frac{a^2}{b}+\frac{b^2}{c} +\frac{c^2}{a}\ge\frac{(a+b+c)^2}{a+b+c}=a+b+c$ donc $LHS\ge2(a+b+ c)$ ## [math-user1, num_likes=1] [quote=math-user2]Par