Plush Wars

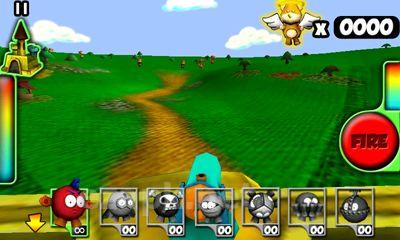
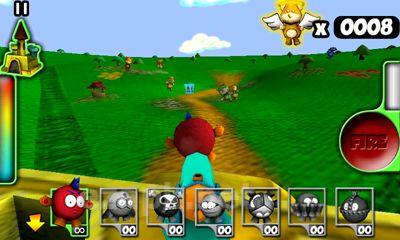
Benvenuto in Plush Wars, dove la tua missione è proteggere il castello della principessa Plushlandia e la principessa stessa da un'invasione di zombi di peluche. In questo paese di peluche, l'unica vera arma è una pistola, mentre tutto il resto, comprese le munizioni, è fatto di materiale di peluche. Da tutte le direzioni, ti troverai di fronte a orsacchiotti e cagnolini che sono stati trasformati in zombi, molto probabilmente a causa dei bambini dispettosi che gli hanno strappato gli occhi, le zampe e la testa. La tua arma preferita è una pistola caricata con proiettili di peluche. Il primo passo è selezionare il bersaglio, quindi premere il pulsante per sparare.<|endoftext|><|endoftext|> # 2015 AMC 10A Problemi/Problema 1. ## Contenuto. 1 problema 2 Soluzione 3 Soluzione video 4 Vedi anche ## Problema Qual è il valore di \[2-4+6-8+10-12+14-16+18-20?\] $\textbf{(A)}\ -10\qquad\textbf{(B)}\ -2\qquad\textbf{(C)}\ 0\qquad\textbf{(D)}\ 2\qquad\textbf{ (E)}\10$ ## Soluzione. Possiamo riorganizzare i termini per ottenere \[2+6+10+14+18-4-8-12-16-20.\] Ora possiamo accoppiare i termini per ottenere \[(2-2)+( 6-4)+(10-8)+(14-12)+(18-16)-20.\] Semplificando, otteniamo \[0+2+2+2+2-20=10-20=\boxed{\textbf{(A)}\ -10}.\] ## Soluzione video. https://youtu.be/8-3XeJXm-qE ~savannahsolver <|endoftext|>## Forum matematici ## Categoria: Olimpiadi delle scuole superiori ## Argomento: disuguaglianza ##Visualizzazioni: 338 ## [inserisci: math-user1, num_posts=697, num_likes_received=372] ## [utente-matematica1, num_mi piace=1] Sia $a,b,c>0$. Dimostralo $\frac{a^2}{b}+\frac{b^2}{c}+\frac{c^2}{a}+3\sqrt[3]{abc}\geq 2(a+b +c)$ ## [inserisci: math-user2, num_posts=545, num_likes_received=72] ## [utente-matematica2, num_mi piace=0] Con AM-GM abbiamo:$\frac{a^2}{b}+\frac{a^2}{b}+b\ge3a$ e simili otteniamo:$\sum_{cyc}\frac{a^2 }{b}+a+b\ge3(a+b+c)$ $\implica$ $\sum_{cyc}\frac{a^2