Block puzzle pop

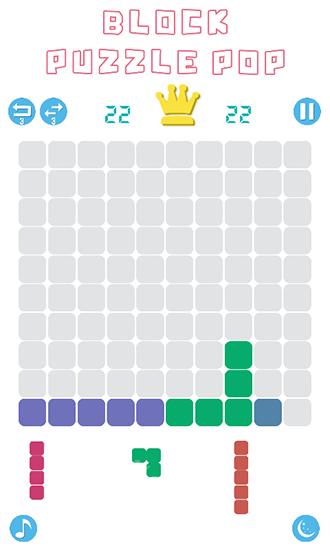
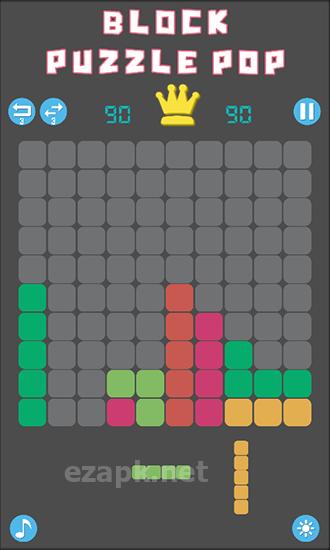
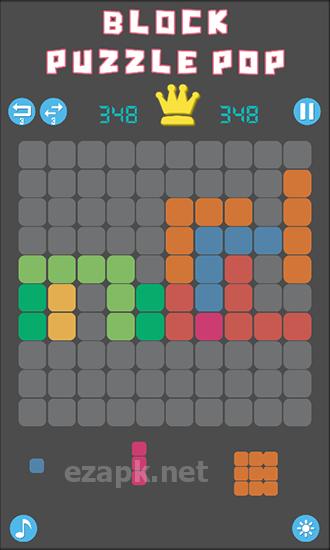
Nel gioco "Block Puzzle Pop", devi posizionare strategicamente blocchi di varie forme, tutti composti da quadrati. Il tuo obiettivo è creare file complete di blocchi per eliminarli. Usa il tuo pensiero logico e la tua immaginazione spaziale per conquistare livelli impegnativi in ​​questo gioco per Android. Nella parte inferiore dello schermo, vedrai tre blocchi che appariranno successivamente. Trascina semplicemente questi blocchi sullo schermo e posizionali in qualsiasi spazio disponibile. Prenditi il ​​tuo tempo e pianifica attentamente le tue mosse, poiché non ci sono limiti di tempo in questo gioco. Le caratteristiche del gioco includono grafica minimalista, modalità giorno e notte, classifiche e 15 obiettivi da sbloccare.<|endoftext|><|endoftext|><|endoftext|> # 2006 AMC 12B Problemi/Problema 1. (Reindirizzato da Problemi AMC 12B del 2006 / Problema 1) ## Problema. Qual è il valore di $2^{-3}+3^{-3}$? $\text {(A) } \frac{5}{9}\qquad \text {(B) } \frac{17}{24}\qquad \text {(C) } \frac{19}{24} \qquad \text {(D) } \frac{7}{8}\qquad \text {(E) } \frac{11}{12}$ ## Soluzione. Possiamo riscrivere $2^{-3}$ e $3^{-3}$ rispettivamente come $\frac{1}{2^3}$ e $\frac{1}{3^3}$. Quindi possiamo combinare le frazioni per ottenere $\frac{1}{8}+\frac{1}{27}$. Possiamo trovare un denominatore comune di $216$ per ottenere $\frac{27}{216}+\frac{8}{216}=\frac{35}{216}$. Possiamo semplificare questa frazione per ottenere $\boxed{\textbf{(B) }\frac{17}{24}}$. <|endoftext|>## Forum matematici ## Categoria: Olimpiadi delle scuole superiori ## Argomento: disuguaglianza ##Visualizzazioni: 351 ## [inserisci: math-user1, num_posts=697, num_likes_received=372] ## [utente-matematica1, num_mi piace=1] Siano $a,b,c$ numeri reali positivi tali che $a+b+c=3$. Dimostralo $\frac{a}{b}+\frac{b}{c}+\frac{c}{a}+3\geq 2(a^2+b^2+c^2)$ ## [inserisci: math-user2, num_posts=467, num_likes_received=180] ## [utente-matematica2, num_mi piace=0] Di AM-GM, $\frac{a}{b}+\frac{a}{b}+\frac{b}{c}\ge3\sqrt[3]{\frac{a^2}{bc} }=\frac{3a}{\sqrt[3]{abc}}$. La somma ciclica dà $\frac{a}{b}+\frac{b}{c