Pixelo

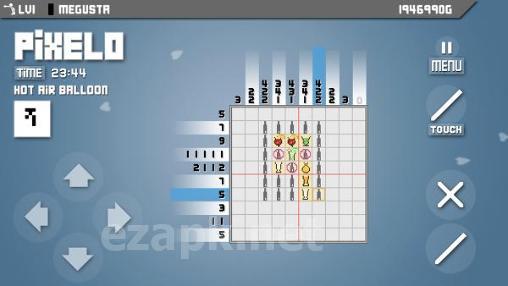
Pixelo è un gioco Android in cui usi la tua logica e l'immaginazione per risolvere i puzzle colorandosi in piastrelle sullo schermo per creare un'immagine. La griglia può variare da 5x5 a 20x20 piastrelle e ogni colonna e riga hanno numeri che indicano quante piastrelle devono essere riempite. I gruppi colorati di piastrelle devono essere separati da almeno una piastrella vuota. Con oltre 500 puzzle, ottima grafica, controlli semplici, punteggi alti e gameplay assorbente, Pixelo è un gioco da non perdere. <| Endoftext |> <| endoftext |> # 2015 AMC 10A Problemi/Problema 1. ## contenuto. 1 problema 2 soluzione 3 soluzione video 4 Vedi anche ## problema Qual è il valore di \ [2-4+6-8+10-12+14-16+18-20+22? \] $ \ textbf {(a)} \ -110 \ qquad \ textbf {(b)} \ -44 \ qquad \ textbf {(c)} \ 0 \ qquad \ textbf {(d)} \ 22 \ qquad \ textbf { (E)} \ 110 $ Soluzione ##. Possiamo riorganizzare i termini per ottenere \ [2+6+10+14+18+22-4-8-12-16-20. \] Ora, possiamo accoppiare i termini per ottenere \ [(2+22) +(6+18)+(10+14) -4-8-12-16-20. \] Semplificazione, otteniamo \ [24+24+24-60 = \ boxed {\ textbf {(c)} \ 0}. \] ## soluzione video. https://youtu.be/8zqng5rzujw ~ Savannahsolver <| endoftext |> ## forum matematici ## Categoria: Olimpiadi delle scuole superiori ## Argomento: disuguaglianza Visualizzazioni ##: 338 ## [Enter: Math-user1, num_posts = 697, num_likes_received = 372] ## [matematica-user1, num_likes = 1] Lascia $ A, B, C> 0 $. Dimostrarlo $ \ frac {a^2} {b}+\ frac {b^2} {c}+\ frac {c^2} {a} +3 \ sqrt [3] {abc} \ geq 2 (a+b +c) $ ## [Enter: Math-user2, num_posts = 545, num_likes_received = 72] ## [matematica-user2, num_likes = 0] Di am-gm ha $ 3 \ sqrt [3] {ABC} \ ge a+b+c $ e di cauchy-schwarz ha $ \ frac {a^2} {b}+\ frac {b^2} {c} +\ frac {c^2} {a} \ ge \ frac {(a+b+c)^2} {a+b+c} = a+b+c $ quindi $ lhs \ ge2 (a+b+ c) $ ## [matematica-user1, num_likes = 1] [QUOTE = Math-User2] di