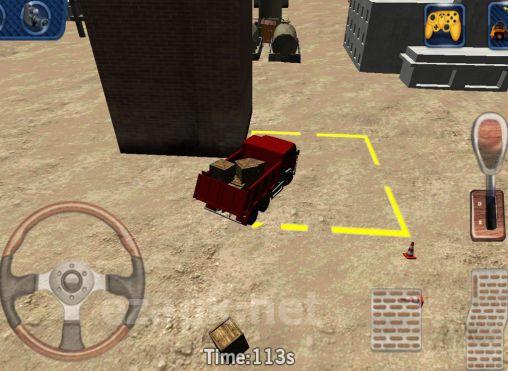
Heavy truck 3D: Cargo delivery

Prova l'emozione di essere un camionista in un cantiere edile con il gioco Heavy Truck 3D: Cargo Delivery. Questo gioco offre 20 livelli entusiasmanti e un sistema di controllo realistico che ti farà sentire come se fossi al volante. Padroneggia le tecniche di parcheggio e scarico più precise e mettiti alla prova con la modalità gioco a tempo.<|endoftext|><|endoftext|> Il termine "anima gemella" è spesso usato per descrivere una persona che è idealmente adatta a un'altra come amica intima o partner romantico. Si ritiene che un'anima gemella sia qualcuno che condivide una profonda connessione con un'altra persona, spesso descritta come un legame spirituale o emotivo. Si dice che questa connessione trascenda l'attrazione fisica e si basi su un forte senso di compatibilità, comprensione e rispetto reciproco. Alcune persone credono che le anime gemelle siano destinate a incontrarsi e che la loro relazione sia destinata a esserlo. Altri vedono le anime gemelle come individui che hanno un profondo impatto sulla vita degli altri, aiutandoli a crescere ed evolversi come individui. In definitiva, il concetto di anima gemella è soggettivo e può significare cose diverse per persone diverse.<|endoftext|>## Forum matematici ## Categoria: Olimpiadi delle scuole superiori ## Argomento: disuguaglianza ##Visualizzazioni: 338 ## [inserisci: math-user1, num_posts=697, num_likes_received=372] ## [utente-matematica1, num_mi piace=1] Sia $a,b,c>0$. Dimostralo $\frac{a^2}{b}+\frac{b^2}{c}+\frac{c^2}{a}+3\sqrt[3]{abc}\geq 2(a+b +c)$ ## [inserisci: math-user2, num_posts=545, num_likes_received=72] ## [utente-matematica2, num_mi piace=0] Con AM-GM abbiamo:$\frac{a^2}{b}+\frac{a^2}{b}+b\ge3a$ e simili otteniamo:$\sum_{cyc}\frac{a^2 }{b}+a+b\ge3(a+b+c)$ e dobbiamo dimostrare che:$3(a+b+c)+3\sqrt[3]{abc}\ge2(a+b+ c)$ $\implica$ $3\sqrt[3]{abc}\ge a+b+c$ che è ovvio per AM-GM ## [utente-matematica1, num_mi piace=1] [quote=math-user2]Con AM-GM abbiamo:$\frac{a^2}{b}+\frac{a^2}{b}+b\ge3a$ e simili otteniamo:$\sum_{cyc }\frac{a^2}{b}+a+b\ge3(a+b+c)$ e dobbiamo dimostrare che:$3(a+b+c)+3\sqrt[3]{abc}\ge2(a+b+c)$ $\implica$ $3\sqrt[3]{abc}\ge a+b+c $ che è ovvio da AM-GM[/quote