Sea Empire: Winter lords

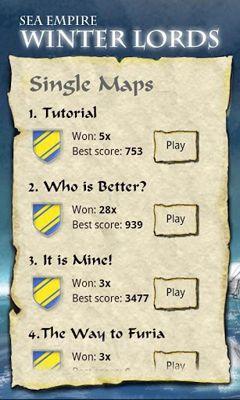
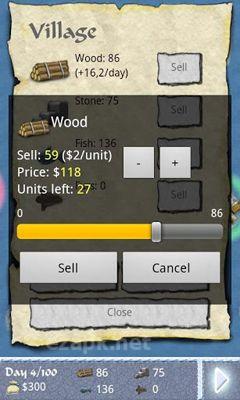
"Partisci alla conquista delle isole vicine in Sea Empire: Winter Lords costruendo una formidabile flotta. Questo gioco vanta una grafica semplice e offre varie opzioni di navi."<|endoftext|><|endoftext|> # 2006 AMC 12B Problemi/Problema 1. (Reindirizzato da Problemi AMC 12B del 2006 / Problema 1) ## Problema. Qual è il valore di $2^{-3}+3^{-3}+4^{-3}+...+2006^{-3}+2007^{-3}$? $\text {(A) } \frac{2007}{2^3} \qquad \text {(B) } \frac{2007^2}{2^3} \qquad \text {(C) } \frac {2007^2+2007}{2^3} \qquad \text {(D) } \frac{2007^2+2007}{2^6} \qquad \text {(E) } \frac{2007^2+2007}{2^7}$ ## Soluzione. Possiamo riscrivere l'espressione come \begin{align*} 2^{-3}+3^{-3}+4^{-3}+...+2006^{-3}+2007^{-3} &= \left(2 ^{-3}+3^{-3}+4^{-3}+...+2006^{-3}\right) + 2007^{-3} \\ &= \sinistra(\frac{1}{2^3}+\frac{1}{3^3}+\frac{1}{4^3}+...+\frac{1}{2006^3} \right) + \frac{1}{2007^3} \\ &= \frac{1}{8}+\frac{1}{27}+\frac{1}{64}+...+\ frac{1}{2006^3} + \frac{1}{2007^3} \\ &= \left(\frac{1}{2^3}\right)^3+\left(\frac{1}{3^3}\right)^ 3+\sinistra(\frac{1}{4^3}\destra)^3+...+\sinistra(\frac{1}{2006^3}\destra)^3 + \left(\frac{1}{2007^3}\right)^3 \\ &= \left(\frac{1}{2^3}+\frac{1}{3^3}+\frac{ 1}{4^3}+...+\frac{1}{2006^3}+\frac{1}{2007^3}\right)^3 \\ &= \left(\frac{1}{8}+\frac{1}{27}+\frac{1}{64}+...+\frac{1}{2006^3}+\frac{1} {2007^3}\right)^3 \\ &= \left(\frac{1}{8}+\frac{1}{27}+\frac