Block puzzle pop

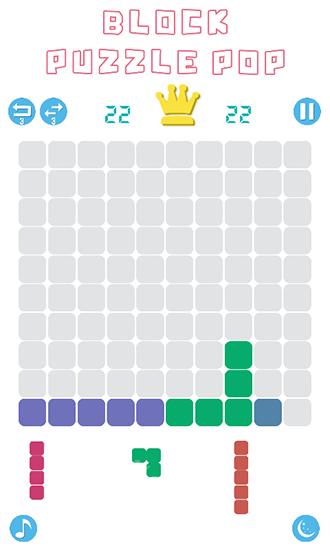
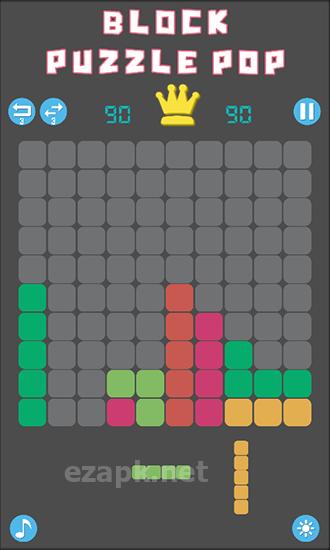
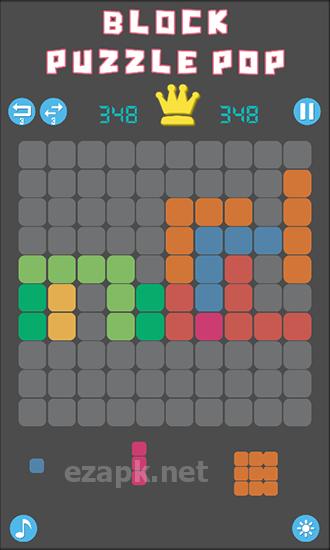
W grze „Block Puzzle Pop” musisz strategicznie umieszczać bloki o różnych kształtach, wszystkie składające się z kwadratów. Twoim celem jest utworzenie pełnych rzędów bloków w celu ich wyeliminowania. Użyj logicznego myślenia i wyobraźni przestrzennej, aby pokonać wymagające poziomy w tej grze na Androida. Na dole ekranu zobaczysz trzy bloki, które pojawią się jako następne. Po prostu przeciągnij te bloki na ekran i umieść je w dowolnym dostępnym miejscu. Nie spiesz się i dokładnie planuj swoje ruchy, ponieważ w tej grze nie ma limitu czasu. Funkcje gry obejmują minimalistyczną grafikę, tryb dzienny i nocny, tabele wyników i 15 osiągnięć do odblokowania.<|endoftext|><|endoftext|><|endoftext|> # 2006 AMC 12B Problemy/Problem 1. (Przekierowano z 2006 AMC 12B Problemy / Problem 1) ## Problem. Jaka jest wartość $2^{-3}+3^{-3}$? $\text {(A) } \frac{5} \qquad \text {(D) } \frac{7}{8}\qquad \text {(E) } \frac{11}{12}$ ## Rozwiązanie. Możemy zapisać $2^{-3}$ i $3^{-3}$ odpowiednio jako $\frac{1}{2^3}$ i $\frac{1}{3^3}$. Następnie możemy połączyć ułamki, aby otrzymać $\frac{1}{8}+\frac{1}{27}$. Możemy znaleźć wspólny mianownik $216$, aby otrzymać $\frac{27}{216}+\frac{8}{216}=\frac{35}{216}$. Możemy uprościć ten ułamek, aby otrzymać $\boxed{\textbf{(B) }\frac{17}{24}}$. <|endoftext|>## Fora matematyczne ## Kategoria: Olimpiady Szkół Średnich ## Temat: Nierówność ## Wyświetlenia: 351 ## [wprowadź: math-user1, num_posts=697, num_likes_received=372] ## [użytkownik matematyczny1, liczba polubień=1] Niech $a,b,c$ będą dodatnimi liczbami rzeczywistymi takimi, że $a+b+c=3$. Udowodnij to $\frac{a}{b}+\frac{b}{c}+\frac{c}{a}+3\geq 2(a^2+b^2+c^2)$ ## [wprowadź: math-user2, num_posts=467, num_likes_received=180] ## [użytkownik matematyczny2, liczba polubień=0] Autor: AM-GM, $\frac{a}{b}+\frac{a}{b}+\frac{b}{c}\ge3\sqrt[3]{\frac{a^2}{bc} }=\frac{3a}{\sqrt[3]{abc}}$. Sumowanie cykliczne daje $\frac{a}{b}+\frac{b}{c