Putter King Adventure Golf

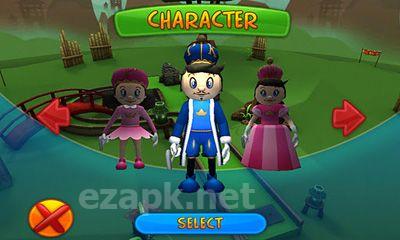
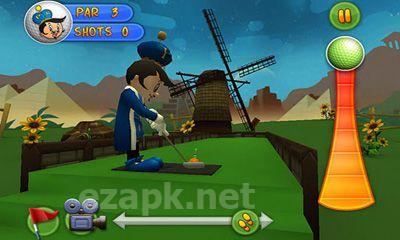
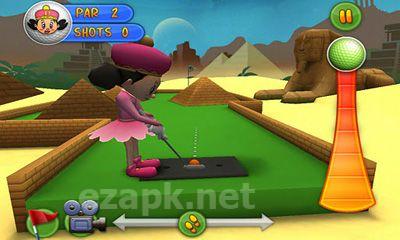
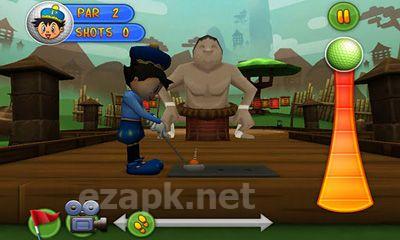
Putter King Adventure Golf to najwyżej oceniana gra w golfa 3D. Zawiera wysokiej jakości grafikę i imponujący dźwięk. Kursy znajdują się na całym świecie. Możesz także udostępnić swoje wyniki znajomym na Facebooku i Twitterze. Wybierz spośród różnych zabawnych animowanych postaci, z których każda ma własne unikalne umiejętności. Twoim celem jest poruszanie się po piłce przez różne przeszkody i do dziury. Gra oferuje 24 odrębne otwory o tematyce, a także 3 otwory utworzone przez użytkowników i 4 tryby gry (mistrzostwo, czas, tryb wieloosobowy i trening). <| Endoftext |> <| Endoftext |> # 2015 AMC 10B Problemy/problem 1. ## Spis treści. 1 problem 2 Rozwiązanie 3 Rozwiązanie wideo 4 Zobacz także ## Problem. Jaka jest wartość 2 USD+4+6+8+10+12+14+16+18+20 $? $ \ textbf {(a)} \ 90 \ qquad \ textbf {(b)} \ 100 \ qquad \ textbf {(c)} \ 110 \ qquad \ textbf {(d)} \ 120 \ qquad \ textbf {(e )} \ 130 $ ## Rozwiązanie. Możemy sparować liczby w następujący sposób: $ (2+20)+(4+18)+(6+16)+(8+14)+(10+12) $. Każda para sumuje się do 22 USD, a para 5 $ $, więc suma wynosi 22 $ \ CDOT 5 = \ boxed {\ textbf {(b)} \ 100} $. ## Rozwiązanie wideo. https://youtu.be/8wrdylw9_ns ~ Savannahsolver <| Endoftext |> ## Mathematical Forum ## Kategoria: Olimpiady w szkole średniej ## Temat: Nierówność ## Widoki: 338 ## [Enter: Math-User1, num_posts = 697, Num_Likes_Received = 372] ## [Math-User1, Num_Likes = 1] Niech $ a, b, c> 0 $. Udowodnić to $ \ frac {a^2} {b}+\ frac {b^2} {c}+\ frac {c^2} {a} +3 \ sqrt [3] {abc} \ geq 2 (a+b +c) $ ## [Enter: Math-User2, num_posts = 545, Num_Likes_Received = 72] ## [Math-User2, Num_Likes = 0] Przez AM-GM mają: $ \ frac {a^2} {b}+\ frac {a^2} {b}+b \ ge3a $ i podobne otrzymujemy: $ \ frac {a^2} {b}++ \ frac {b^2} {c}+\ frac {c^2} {a} \ ge a+b+c $ i przez am-gm ponownie: $ 3 $ sqrt [3] {abc} \ ge3 \ frac { 3abc} {a+b+c} $, więc powinniśmy udowodnić, że: $ \ frac {a^2} {b}+\ frac {b^2} {c}+\ frac {c^2} {a}