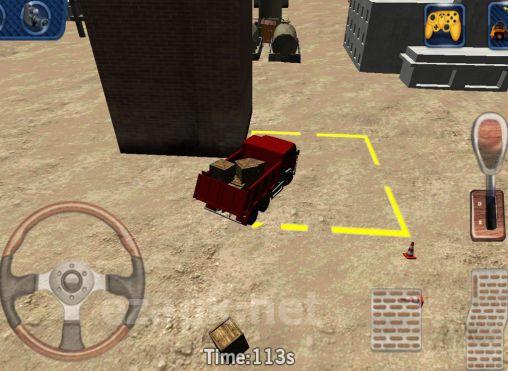
Heavy truck 3D: Cargo delivery

Poczuj dreszczyk emocji związany z byciem kierowcą ciężarówki na placu budowy w grze Heavy Truck 3D: Cargo Delivery. Ta gra oferuje 20 ekscytujących poziomów i realistyczny system sterowania, który sprawi, że poczujesz się jak za kierownicą. Opanuj najbardziej precyzyjne techniki parkowania i rozładunku i rzuć sobie wyzwanie w trybie gry na czas.<|endoftext|><|endoftext|> Termin „bratnia dusza” jest często używany do opisania osoby, która idealnie pasuje do innej osoby jako bliski przyjaciel lub partner romantyczny. Uważa się, że bratnia dusza to osoba posiadająca głęboką więź z inną osobą, często opisywaną jako więź duchowa lub emocjonalna. Mówi się, że to połączenie wykracza poza pociąg fizyczny i opiera się na silnym poczuciu zgodności, zrozumienia i wzajemnego szacunku. Niektórzy ludzie wierzą, że przeznaczeniem bratnich dusz jest się spotkać i że ich związek ma taki być. Inni postrzegają bratnie dusze jako jednostki, które mają głęboki wpływ na życie innych, pomagając im wzrastać i ewoluować jako jednostki. Ostatecznie pojęcie bratniej duszy jest subiektywne i dla różnych ludzi może oznaczać co innego.<|endoftext|>## Fora matematyczne ## Kategoria: Olimpiady Szkół Średnich ## Temat: Nierówność ## Wyświetlenia: 338 ## [wprowadź: math-user1, num_posts=697, num_likes_received=372] ## [użytkownik-matematyczny1, liczba_polubień=1] Niech $a,b,c>0$. Udowodnij to $\frac{a^2}{b}+\frac{b^2}{c}+\frac{c^2}{a}+3\sqrt[3]{abc}\geq 2(a+b +c)$ ## [wprowadź: math-user2, num_posts=545, num_likes_received=72] ## [użytkownik matematyczny2, liczba polubień=0] Według AM-GM mamy:$\frac{a^2}{b}+\frac{a^2}{b}+b\ge3a$ i podobnie otrzymujemy:$\sum_{cyc}\frac{a^2 }{b}+a+b\ge3(a+b+c)$ i musimy udowodnić, że:$3(a+b+c)+3\sqrt[3]{abc}\ge2(a+b+ c)$ $\implies$ $3\sqrt[3]{abc}\ge a+b+c$ co jest oczywiste dla AM-GM ## [użytkownik matematyczny1, liczba polubień=1] [quote=math-user2]Przez AM-GM mamy:$\frac{a^2}{b}+\frac{a^2}{b}+b\ge3a$ i podobnie otrzymujemy:$\sum_{cyc }\frac{a^2}{b}+a+b\ge3(a+b+c)$ i musimy udowodnić to:$3(a+b+c)+3\sqrt[3]{abc}\ge2(a+b+c)$ $\implies$ 3\sqrt[3]{abc}\ge a+b+c $ co jest oczywiste dla AM-GM[/quote