Plush Wars

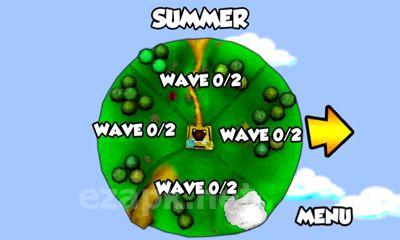
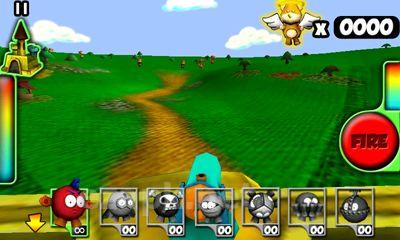
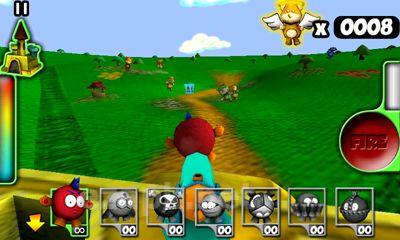
Bem-vindo ao Plush Wars, onde sua missão é proteger o castelo da Princesa Plushlandia e a própria princesa de uma invasão de zumbis de pelúcia. Neste país de pelúcia, a única arma real é uma pistola, enquanto todo o resto, incluindo munições, é feito de material de pelúcia. De todas as direções, você se deparará com ursinhos de pelúcia e cachorrinhos que foram transformados em zumbis, provavelmente devido a crianças travessas arrancando seus olhos, patas e cabeças de botão. Sua arma preferida é uma arma carregada com balas de pelúcia. O primeiro passo é selecionar seu alvo e, em seguida, pressionar o botão para disparar.<|endoftext|><|endoftext|> # 2015 Problemas AMC 10A/Problema 1. ## Conteúdo. 1 problema 2 Solução 3 solução de vídeo 4 Veja também ## Problema Qual é o valor de \[2-4+6-8+10-12+14-16+18-20?\] $\textbf{(A)}\ -10\qquad\textbf{(B)}\ -2\qquad\textbf{(C)}\ 0\qquad\textbf{(D)}\ 2\qquad\textbf{ (E)}\ 10$ ## Solução. Podemos reorganizar os termos para obter \[2+6+10+14+18-4-8-12-16-20.\] Agora, podemos emparelhar os termos para obter \[(2-2)+( 6-4)+(10-8)+(14-12)+(18-16)-20.\] Simplificando, obtemos \[0+2+2+2+2-20=10-20=\boxed{\textbf{(A)}\ -10}.\] ## Solução de vídeo. https://youtu.be/8-3XeJXm-qE ~savannahsolver <|endoftext|>## Fóruns Matemáticos ## Categoria: Olimpíadas do Ensino Médio ## Tópico: Desigualdade ## Visualizações: 338 ## [insira: math-user1, num_posts=697, num_likes_received=372] ## [math-user1, num_likes=1] Seja $a,b,c>0$. Prove isso $\frac{a^2}{b}+\frac{b^2}{c}+\frac{c^2}{a}+3\sqrt[3]{abc}\geq 2(a+b +c)$ ## [insira: math-user2, num_posts=545, num_likes_received=72] ## [math-user2, num_likes=0] Por AM-GM temos:$\frac{a^2}{b}+\frac{a^2}{b}+b\ge3a$ e semelhantes obtemos:$\sum_{cyc}\frac{a^2 }{b}+a+b\ge3(a+b+c)$ $\implica$ $\sum_{cyc}\frac{a^2