Block puzzle pop

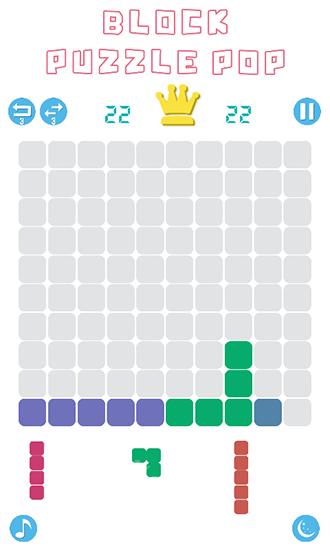
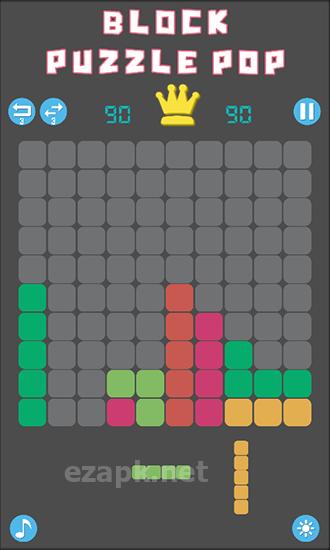
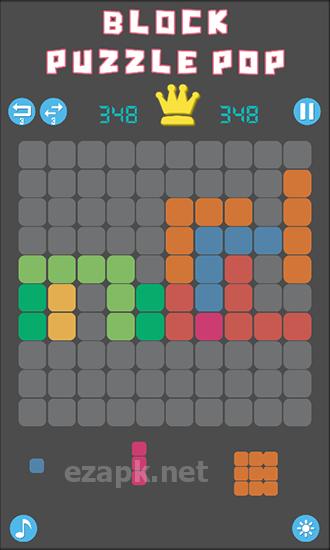
No jogo "Block Puzzle Pop", você deve colocar estrategicamente blocos de várias formas, todos compostos de quadrados. Seu objetivo é criar linhas completas de blocos para eliminá -los. Use seu pensamento lógico e imaginação espacial para conquistar níveis desafiadores neste jogo do Android. Na parte inferior da tela, você verá três blocos que aparecerão a seguir. Basta arrastar esses blocos para a tela e posicioná -los em qualquer espaço disponível. Tome seu tempo e planeje cuidadosamente seus movimentos, pois não há limite de tempo neste jogo. Os recursos do jogo incluem gráficos minimalistas, um modo diurno e noturno, tabelas de classificação e 15 realizações para desbloquear. # 2006 AMC 12B Problemas/Problemas 1. (Redirecionado de 2006 AMC 12b Problemas / Problema 1) ## Problema. Qual é o valor de $ 2^{-3} +3^{-3} $? $ \ text {(a)} \ frac {5} {9} \ qquad \ text {(b)} \ frac {17} {24} \ qquad \ text {(c)} \ frac {19} {24}} \ qquad \ text {(d)} \ frac {7} {8} \ qquad \ text {(e)} \ frac {11} {12} $ ## Solução. Podemos reescrever $ 2^{-3} $ e $ 3^{-3} $ como $ \ frac {1} {2^3} $ e $ \ frac {1} {3^3} $, respectivamente. Em seguida, podemos combinar as frações para obter $ \ frac {1} {8}+\ frac {1} {27} $. Podemos encontrar um denominador comum de $ 216 $ para obter $ \ frac {27} {216}+\ frac {8} {216} = \ frac {35} {216} $. Podemos simplificar essa fração para obter $ \ boxed {\ textbf {(b)} \ frac {17} {24}} $. <| endoftext |> ## fóruns matemáticos Categoria ##: Olimpiads do ensino médio ## Tópico: desigualdade Visualizações ##: 351 ## [enter: math-user1, num_posts = 697, num_likes_received = 372] ## [math-user1, num_likes = 1] Seja $ A, B, C $ Números reais positivos, de modo que $ A+B+C = 3 $. Provar isso $ \ frac {a} {b}+\ frac {b} {c}+\ frac {c} {a} +3 \ geq 2 (a^2+b^2+c^2) $ ## [enter: math-user2, num_posts = 467, num_likes_received = 180] ## [Math-User2, num_likes = 0] Por am-gm, $ \ frac {a} {b}+\ frac {a} {b}+\ frac {b} {c} \ ge3 \ sqrt [3] {\ frac {a^2} {bc} } = \ frac {3a} {\ sqrt [3] {abc}} $. A soma ciclicamente fornece $ \ frac {a} {b}+\ frac {b} {c