Heavy truck 3D: Cargo delivery

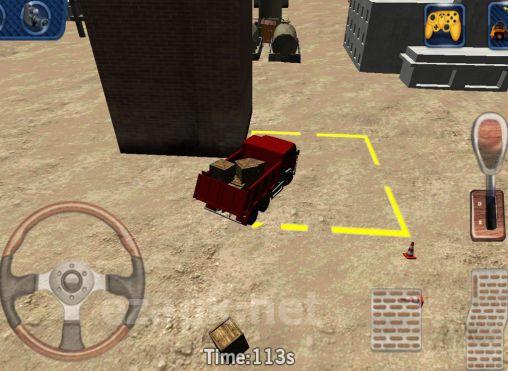
Experimente a emoção de ser um motorista de caminhão em um canteiro de obras com o Game Heavy Truck 3D: entrega de carga. Este jogo oferece 20 níveis emocionantes e um sistema de controle realista que fará com que você se sinta atrás do volante. Domine as técnicas de estacionamento e descarregamento mais precisas e desafie -se com o modo de jogo do tempo. <| EndofText |> <| endofText |> O termo "alma gêmea" é frequentemente usado para descrever uma pessoa que é ideal para outra como um amigo próximo ou parceiro romântico. Acredita -se que uma alma gêmea seja alguém que compartilha uma conexão profunda com outra pessoa, muitas vezes descrita como um vínculo espiritual ou emocional. Diz -se que essa conexão transcende a atração física e é baseada em um forte senso de compatibilidade, compreensão e respeito mútuo. Algumas pessoas acreditam que as almas gêmeas estão destinadas a se encontrar e que seu relacionamento deve ser. Outros veem almas gêmeas como indivíduos que têm um profundo impacto na vida um do outro, ajudando -os a crescer e evoluir como indivíduos. Por fim, o conceito de alma gêmea é subjetivo e pode significar coisas diferentes para pessoas diferentes. <| EndofText |> ## fóruns matemáticos Categoria ##: Olimpiads do ensino médio ## Tópico: desigualdade Visualizações ##: 338 ## [enter: math-user1, num_posts = 697, num_likes_received = 372] ## [math-user1, num_likes = 1] Seja $ A, B, C> 0 $. Provar isso $ \ frac {a^2} {b}+\ frac {b^2} {c}+\ frac {c^2} {a} +3 \ sqrt [3] {abc} \ geq 2 (a+b +c) $ ## [enter: math-user2, num_posts = 545, num_likes_received = 72] ## [Math-User2, num_likes = 0] Por am-gm tem: $ \ frac {a^2} {b}+\ frac {a^2} {b}+b \ ge3a $ e similar: $ \ sum_ {cyc} \ frac {a^2 } {b}+a+b \ ge3 (a+b+c) $ e precisamos provar que: $ 3 (a+b+c) +3 \ sqrt [3] {abc} \ ge2 (a+b+ c) $ $ \ implica $ $ 3 \ sqrt [3] {ABC} \ ge A+B+C $, que é óbvio por AM-GM ## [math-user1, num_likes = 1] [QUOTE = Math-user2] Por AM-GM tem: $ \ frac {a^2} {b}+\ frac {a^2} {b}+b \ ge3a $ e similar nós: $ \ sum_ {cyc {cyc } \ frac {a^2} {b}+a+b \ ge3 (a+b+c) $ e precisamos provar que: $ 3 (a+b+c) +3 \ sqrt [3] {abc} \ ge2 (a+b+c) $ $ \ implica $ $ 3 \ sqrt [3] {abc} \ ge a+b+c $, que é óbvio por am-gm [/citação